Big Data, Small Machine
Introduction
I was honored to be invited by DevTO to give a talk at their May meetup. The organizers were keen to have someone speak about high-performance machine learning, and I was happy to oblige.
The general thesis of the talk is that, for the purposes of machine learning, setting up large compute clusters is wholly unnecessary. Furthermore, it should generally be considered harmful as those efforts are extremely time consuming and detract from solving the actual machine learning problem at hand.
To illustrate the point, I showed an online learning approach to binary classification problems using logistic regression with adaptive learning rates. While some might dismiss this approach as too simplistic or ineffective, consider that it is not very different from what Google was (is?) using for some of their online advertising prediction systems. This was described in the wonderful paper Ad Click Prediction: a View from the Trenches.
As in previous summaries of my lectures, I’ll reference select slides by section header and provide the explanation that went along with the slide, including some elaboration I may not have had time for in the lecture itself.
Claims
In my lecture I made a few general claims:
- RAM in machines used to process data is growing more quickly than the data itself
- There are many techniques for dealing with so-called Big Data and none of which involve clusters or heavy data infrastructure components like Kafka, Hadoop, Spark, and so on
- One machine is fine for machine learning tasks, i.e., actually training ML models
Step 0: More RAM
If you have a data set that is too big to fit into memory, you can consider getting access to more memory.
We know from other articles and surveys done by KDnuggets that the size of data sets people actually analyze seems to be growing at around 20% per year. Additionally, this data tells us that most analytics professionals deal with data sets that are below 100GB or so in size.
We also know from looking at historical RAM availability on EC2 instances (just as an example) that the yearly increase in RAM on these instances is faster than the 20% yearly increase in data set size.
| Year | Type | RAM (GiB) |
|---|---|---|
| 2007 | m1.xlarge | 15 |
| 2009 | m2.4xlarge | 68 |
| 2012 | hs1.8xlarge | 117 |
| 2014 | r3.8xlarge | 244 |
| 2016 | x1.32xlarge | 1952 |
| 2017/8 | x1e.32xlarge | 3904 |
So for a lot of people, a single AWS instance circa 2012 would have been sufficient to perform all the necessary work for a machine learning task. Nevermind of course, that the currently available high memory instances provide 4TB of RAM, which is far more than the data set sizes most analytics professionals deal with.
Lastly, note that Tyan makes a motherboard which can currently accomodate 12.3TB of RAM, which is up from 6TB around 2016.
When all this is taken together, most people can do all the analytics and machine learning tasks they need to do on a single machine with adequate memory. This completely obviates the need for infrastructure like Hadoop, Spark, and so on for training machine learning models (though they may have their place in preprocessing).
Step 1: Sampling
Consider though that perhaps you still have too much data to fit into RAM, or you simply want to train your model more quickly with approximately the same level of accuracy. In that case, just don’t use all the available training data!
In the last years, it has somehow become fashionable to completely ignore centuries of mathematical and statistical progress and instead insist that, in order to make a useful model, all data must be analyzed. This perspective became even more generally accepted in the last decade or so, and especially after Halevy, Norvig, and Periera published The Unreasonable Effectiveness of Data (PDF).
Truths to having a larger training set notwithstanding, just because a larger data set for training may yield better results does not mean that using the larger training set yields significantly better results. Often, the marginal increase in performance of a machine learning model from adding additional data is just not worth the additional annoyance of having to deal with the more complicated methods and infrastructure components that may be required to use all of the data.
More data might beat better algorithms, as the saying goes, but perhaps not by much.
This problem is particularly clear in the online advertising space and predicting clicks on advertisements. It is not unusual to display an advertisement 10,000 times in order to achieve just 20 clicks. In other words, approximately 99.8% of the data set will be views of ads that do not result in a click.
With a data set that has such biased class distribution, you could probably randomly eliminate 90% of the views and still have a similar performance from your classifier. In other words, if you had 100GB of training data, you would only have to bother with processing 10GB instead. This of course requires nothing particularly special in terms of hardware, and can be completed on many modern laptops.
What if sampling doesn’t work? Try streaming!
There might be cases when sampling isn’t an option, or won’t work for some reason, and the data is too large to fit into RAM.
In other words, we will transform the problem from a batch-based approach of training a model on a set of data to an online-based approach where our model is learning as it receives data from a stream. Think about it like building a system that takes requests to feed the model learning information, or obtain a prediction, instead of a model that takes in a large chunk of data in order to calculate model weights. In doing this, we also change from a focus of how much data our model can handle at one time, to how many Requests Per Second (RPS) our system is capable of handling. Higher RPS means we can handle more data, in less time.
To think in terms of streams with machine learning models, we need three basic things:
- A data source that can emit requests/events
- A method of stateless feature extraction, so that obtaining features doesn’t depend on other requests in the (potentially infinite) stream
- A machine learning model that supports incremental learning
Data Source
If we have a large file, we can simply read it in one record/request at a time. A simple way of doing this with a generator in Python might look something like:
def getRequest(path, numFeatures):
count = 0
for i, line in enumerate(open(path)):
if i == 0:
# do whatever you want at initialization
x = [0] * numFeatures # So we don't need to create a new x every time
continue
for t, feat in enumerate(line.strip().split(',')):
if t == 0:
y = feat # assuming first position in request is some kind of label
else:
# do something with the features
x[m] = feat
yield (count, x, y)
Or alternatively, if we are using Pandas we can simply pass in the chunksize parameter to a method like read_csv():
reader = pd.read_csv('blah.csv', chunksize=10000)
for chunk in reader:
doSomething(chunk)
That covers the need to transform a file that is too large to fit into memory into a stream of data we can easily process.
Stateless Feature Extraction
Hello, hashing trick!
This slide was a bit difficult to fully explain given the time constraints of the lecture and density of the information. The short version is that we will convert a request into an array of integers by concatenating each feature name and value in the request, and then taking a hash of that result.
For example, if the feature is firstName and the value is Adam then we would hash firstNameAdam and obtain some number, say 18445008. This number will then serve as the index for that particular feature name/feature value combination in our array of weights in our model. This allows us to do a few extremely important things in a large-scale/sparse learning scenario:
- We do not need to know the features in advance, since a feature name/value combination always reliably hashes to the same weight
- By deciding how many weights (
modelWeights) we want our model to have up front, likely dictated by our RAM constraints, we can control RAM usage very precisely by simply taking the hash modulo the number of weights18445008 % modelWeights. - Since we are not storing any mappings between features and values and so on, we can save a lot of additional RAM. We can simply adjust weights in the model by going to the resulting index in the weights array directly from the hash.
With the above in mind, the hashing trick is a very important and useful tool when data is large but RAM is in tight supply. This is equally true on smaller systems like embedded devices, which will become increasingly popular as analytics tasks are more distributed. Embedded devices also typically do not have nearly as much RAM as a large EC2 instance. If you only have an embedded device with 10MB of RAM to spare, you can simply limit the number of weights in your model accordingly. It’s amazing how accurate a model you can produce if you are using 32 bit floats and have 4MB of memory available.
Incremental Learning
Once we have the stream and the hashing trick on hand (if needed) we can provide the features to our model N request at a time, or even one request at a time, as long as the model is one that supports incremental learning. There are many such models available in scikit-learn, but here we will just use our own in the form of logistic regression with adaptive learning rates.
# Turn the request into a list of hash values
x = [0] # 0 is the index of the bias term
for key, value in request.items():
index = int(value + key[1:], 16) % D
x.append(index)
# Get the prediction for the given request (now transformed to hash values)
wTx = 0.
for i in x: # do wTx
wTx += w[i] # w[i] * x[i], but if i in x we got x[i] = 1.
p = 1. / (1. + exp(-max(min(wTx, 20.), -20.)))
# Update the loss
p = max(min(p, 1. - 10e-12), 10e-12)
loss += -log(p) if y == 1. else -log(1. - p)
# Update the weights
for i in x:
# alpha / (sqrt(n) + 1) is the adaptive learning rate heuristic
# (p - y) * x[i] is the current gradient
# note that in our case, if i in x then x[i] = 1
w[i] -= (p - y) * alpha / (sqrt(n[i]) + 1.)
n[i] += 1.
To the best of my recollection, this code was originally provided by tinrtgu on the Kaggle forums some years ago, and it’s a great example of how to do machine learning with limited RAM.
Performance
V1
In testing on my laptop with some old data, I was able to use the above code to train a model at a rate of ~20,000 RPS. This is respectable, and there are few people who have to deal with online machine learning systems that have to handle more load than that. However, that’s usually the kind of situation that causes companies to contact me for technical help, so I explored further.
V2
What’s the first thing someone should do when CPython isn’t fast enough? Try PyPy!
Simply by running the script with PyPy instead of the regular CPython interpreter, I got a performance increase of 3.5x (74,000 RPS vs 20,000 RPS).
I cannot overemphasize how important this step is if your company uses Python in your data processing activities and things are too slow. You may be able to speed them up dramatically without making a single modification to your code, thus allowing you to work on other important business problems. If your Python is too slow, TRY PYPY!
V3
One problem with Python in these scenarios is that Python is single-threaded by default and therefore will not avail itself of additional processor cores on the machine. We’d really like to use all cores, and just place some locks around the critical weight arrays so as to prevent non-atomic modifications by multiple threads or processes.
However, due to the Global Interpreter Lock (GIL) in CPython, only a single Python thread can execute bytecode at any given time. Because of that, we have to spawn multiple processes using the multiprocessing library. In this scenario, each process is essentially running its own copy of the Python interpreter. Then you can do things like use a RawArray from multiprocessing.sharedctypes if you want to have multiple processes operate on a single chunk of memory.
from multiprocessing.sharedctypes import RawArray
from multiprocessing import Process
import time
import random
def incr(arr, i):
time.sleep(random.randint(1, 4))
arr[i] += 1
print(arr[:])
arr = RawArray('d', 10)
procs = [Process(target=incr, args=(arr,i)) for i in range(10)]
for p in procs:
p.start()
for p in procs:
p.join()
'''
[0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0]
[0.0, 1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0]
[0.0, 1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0]
[0.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 0.0]
[0.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 0.0]
[0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 0.0]
[0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0]
[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0]
[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]
'''
In practice, the standard way to handle this would be to place the requests we want to process into a work queue, and then have multiple worker processes pull from the queue and do all the processing tasks from the code in the Incremental Learning section above. This looks something like the following.
from multiprocessing import Queue
procs = [Process(target=worker, args=(q, w, n, D, alpha, loss, count,)) \
for x in range(4)]
for p in procs:
p.start()
for t, row in enumerate(DictReader(open(train))):
q.put(row)
Bad news…
Unfortunately, the code above is actually slower than the single-threaded version. Why, you ask?
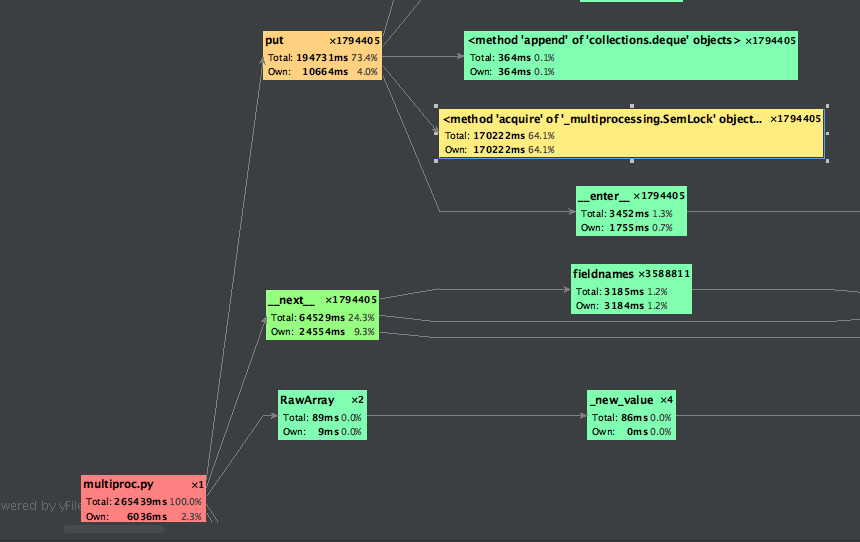
If we have a look at the call graph above, we can see that we’re spending about 64% of the run time waiting to acquire access to the queue. This is a common issue in multi-threaded programming, and while it could be potentially, partially, ameliorated by doing things like putting more than one request in the queue at a time (i.e., using a mini-batch approach), the fact is that we’re having to do a lot of gymnastics to make Python faster at this point. For such a small program, maybe Python isn’t the best tool for the job.
V4 - Hello Go!
Thankfully, Go is a pretty straightforward language, and also reasonably fast. For a program like this, it could be a good fit. We can easily port the Python version of the code over to Go. Besides the braces, it looks about the same.
// Hash the request values
for i, v := range request {
hashResult := hash([]byte(fields[i] + v)) % int(D)
x[i+1] = int(math.Abs(float64(hashResult)))
}
// Get the prediction for the given request (now transformed to hash values)
wTx := 0.0
for _, v := range x {
wTx += (*w)[v]
}
p := 1.0 / (1.0 + math.Exp(-math.Max(math.Min(wTx, 20.0), -20.0)))
// Update the loss
p = math.Max(math.Min(p, 1.-math.Pow(10, -12)), math.Pow(10, -12))
if y == 1 {
*loss += -math.Log(p)
} else {
*loss += -math.Log(1.0 - p)
}
// Update the weights
for _, v := range x {
(*w)[v] = (*w)[v] - (p-float64(y))*alpha/(math.Sqrt((*n)[v])+1.0)
(*n)[v]++
}
This port of the model runs at 186,000 RPS, which is about a 9x speedup over the CPython version! For most companies or purposes, we could simply stop here since most of the time anything more than an order of magnitude speedup isn’t required before moving on to the next bottleneck. However, we can still do better!
V5 - Multicore!
Now we’re getting somewhere.
Since we’re using Go instead of CPython, it’s now trivial to run our code across all of our processor cores. We simple wrap the code above in a function called worker and then we spawn multiple workers which consume our input and do the processing. We also make sure to use a sync.Mutex to lock the shared memory so as to prevent multiple processes writing from memory or corrupting things.
for i := 0; i < 5; i++ {
wg.Add(1)
go worker(input, fields, &w, &n, D, alpha, &loss, &count, &wg, mutex)
}
This gets us further improvement, with the resulting processing speed being 253,000 RPS.
More efficient locking?
The Go version of our code is much faster than our original CPython version (and the PyPy) version, which makes sense as it is a faster language in general and is also using multiple CPU cores. However, we’re still being slowed down due to the workers having to wait to acquire locks before they can update the weights in our model.
It’s definitely worth asking how to make that faster, and there are certainly ways to go about that. One example could be round-robin updates as described in this NIPS paper.
However, it could also be worth asking a different question.
What if we just ditch the locks?
This is the question examined in the paper HOGWILD!: A Lock-Free Approach to Parallelizing Stochastic Gradient Descent.
The short answer is that when you are dealing with sparse data, as we are in this case, you can just remove the locks and let your processes run hog wild on the memory (hence the name) without any issues. In fact, any collisions or erroneous updates that do happen seem to add a kind of smoothing effect, resulting in the models performing better than predicted!
So what happens to our code if we remove the locks from the workers?
V6 - HOGWILD!
import (
"fmt"
"hash/fnv"
"math"
"strings"
"sync"
"time"
fstream "github.com/adamdrake/gofstream"
)
func hash(s []byte) int {
h := fnv.New64a()
h.Write(s)
return int(h.Sum64())
}
func worker(recs chan string, fields []string, w, n *[]float64, D, alpha float64, loss *float64, count *int, wg *sync.WaitGroup) {
defer wg.Done()
for r := range recs {
request := strings.Split(r, ",")
*count++
y := 0
if request[1] == "1" {
y = 1
}
request = request[2:] // ignore label and id
x := make([]int, len(request)+1) // need length plus one for zero at front
x[0] = 0
for i, v := range request {
hashResult := hash([]byte(fields[i]+v)) % int(D)
x[i+1] = int(math.Abs(float64(hashResult)))
}
// Get the prediction for the given request (now transformed to hash values)
wTx := 0.0
for _, v := range x {
wTx += (*w)[v]
}
p := 1.0 / (1.0 + math.Exp(-math.Max(math.Min(wTx, 20.0), -20.0)))
// Update the loss
p = math.Max(math.Min(p, 1.-math.Pow(10, -12)), math.Pow(10, -12))
if y == 1 {
*loss += -math.Log(p)
} else {
*loss += -math.Log(1.0 - p)
}
// Update the weights
for _, v := range x {
(*w)[v] = (*w)[v] - (p-float64(y))*alpha/(math.Sqrt((*n)[v])+1.0)
(*n)[v]++
}
}
}
func main() {
start := time.Now()
D := math.Pow(2, 20) // number of weights use for learning
alpha := 0.1 // learning rate for sgd optimization
w := make([]float64, int(D))
n := make([]float64, int(D))
loss := 0.0
count := 0
data, _ := fstream.New("../train.csv", 10000)
fields := strings.Split(<-data, ",")
var wg sync.WaitGroup
for i := 0; i < 5; i++ {
wg.Add(1)
go worker(data, fields, &w, &n, D, alpha, &loss, &count, &wg)
}
wg.Wait()
fmt.Println("Run time is", time.Since(start))
fmt.Println("loss", loss/float64(count))
fmt.Println("RPS", float64(count)/time.Since(start).Seconds())
}
The code above gets us to 366,000 RPS on my laptop, which has an 18x speedup over the CPython version. The Go code is also not optimized, and could pretty easily be made even faster.
As a side node, the solution above is not completely lock-free, as there is still locking going on from the buffered channel data.
Conclusion
There has been quite a bit of hype surrounding Big Data and the tooling required to deal with it, largely from companies whose entire business model revolves around selling you the tools to processes larger data sets. However, in many cases those tools are completely unnecessary and harmful to the focus and priorities of your development teams, not to mention your budget. As an example, see a previous article of mine where I did a quick demonstration of how simple command-line tools on a laptop can be 235x faster than a Hadoop cluster.
What we’ve really done above is transform a batch-oriented machine learning problem into a streaming/online learning problem. This provides us with much more flexibility in terms of how much memory is required to achieve the objective (in this case, binary classification) and is wholly independent of input data size. Transforming problems like this into stream-based problems is a very valuable technique.
In this article we’ve seen that it’s relatively easy to deal with data sets larger than your RAM, or in fact infinitely large. Using these techniques, you can probably process the data at a rate limited only by the read speed of your SSD!
